Can You Find the Determinant of a Non Square Matrix

The determinant of a 3x3 matrix (General and Shortcut method)

As we take seen in past lessons, in guild to ascertain what is a determinant of a matrix nosotros demand to go dorsum a to our definition of a matrix. Recollect that we have learnt that a matrix is an ordered listing of numbers put in a rectangular bracket. This list can too exist called a rectangular array, and it provides an orderly fashion to display a "list" of data elements. If you want to review the definition of the matrix with more item you lot tin revisit our lesson on note of matrices.

A matrix describes a linear transformation or linear map, which is a kind of transcription between two types of algebraic structures, such as vector fields. In that way, nosotros tin resolve systems of linear equations by representing a linear arrangement as a matrix. The matrix representation of a linear system is fabricated by using all of the variable coefficients plant in the system, and employ them equally element entries to construct the rectangular array of an advisable size augmented matrix. In such matrix, the results of each equation from the system will be placed on the correct manus side of the vertical line which represents the equal sign.

Knowing that, this lesson will focus on the process for evaluating the determinant of a 3x3 matrix and the ii possible methods to employ.

What is the determinant of a matrix

By using the knowledge that a matrix is an array containing the information of a linear transformation, and that this assortment can be conformed by the coefficients of each variable in an equation organization, we tin can describe the function of a determinant: a determinant will scale the linear transformation from the matrix, it will permit us to obtain the inverse of the matrix (if in that location is one) and information technology will assist in the solution of systems of linear equations past producing conditions in which we can expect certain results or characteristics from the organization (depending on the determinant and the type of linear arrangement, we tin know if we may expect a unique solution, more than one solution or none at all for the system).

But there is a condition to obtain a matrix determinant, the matrix must exist a foursquare matrix in order to summate it. Hence, the simplified definition is that the determinant is a value that can be computed from a square matrix to aid in the resolution of linear equation systems associated with such matrix. The determinant of a non square matrix does not be, merely determinants of square matrices are defined mathematically.

The determinant of a matrix tin can exist denoted simply every bit det A, det(A) or |A|. This last notation comes from the notation nosotros directly employ to the matrix we are obtaining the determinant of. In other words, we usually write down matrices and their determinants in a very similar manner:

Equation one: Difference between the notation of a matrix and a determinant

Notice the difference, the matrix is written downward with rectangular brackets and the determinant of the matrix has its components surrounded past two straight lines.

The lesson of today will be focused on the procedure to compute the determinant of a 3x3 matrix, taking approach of the matrix determinant backdrop, which take been briefly seen in past lessons. Remember we volition look at that complete topic in a later lesson chosen: backdrop of determinants. Notwithstanding, information technology is of import to go along those backdrop in mind while performing the calculations of the exercises in the concluding department of this lesson.

How to observe the determinant of a 3x3 matrix

There are two methods for finding the determinant of a 3x3 matrix: the general method and the shortcut method. Just as the names of each of them audio, the general method is the "formal" method to use mathematically, following all the rules and producing some minor matrix determinant calculations forth the mode to find the final solution. While the shortcut method is more of a clever trick we can use to simplify the calculation, still beingness careful to non forget numbers, the guild in which they have to exist multiplied and some rearrangements of the elements in the matrix.

After you take a look at both methods to find the determinant of a 3x3 matrix, you can always selection whichever suits you best and use it for your studies, but remember that information technology is important you know both of them in example you are ever asked to compare results from them.

So, without farther delay let u.s.a. define the determinant of 3x3 matrix A equally shown below, so we can observe how it tin be calculated through both methods:

Equation ii: Determinant of matrix A

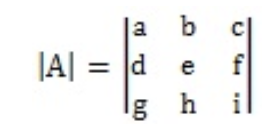
• General method

  The general method to obtain the determinant of a 3x3 matrix consists of breaking down the matrix into secondary matrices of smaller dimensions in a process called "expansion of the first row". What this process does is to utilize the elements from the first row of the 3x3 matrix and use them as factors in a sum of multiplications where the big matrix gets redistributed.

  Let the states go get step by footstep on how to calculate the determinant of a 3x3 matrix:

  1. Y'all showtime take the first element of the first row and multiply it past a secondary 2x2 matrix which comes from the elements remaining in the 3x3 matrix that do not vest to the row or cavalcade to which your first selected element belongs.

     Taking as a reference the 3x3 matrix determinant shown in equation 2, we construct the first function of the outcome of this operation by selecting the outset chemical element of the first row and column (which is abiding "a"), and and so multiply information technology by a matrix produced from the four elements which do not vest to either the row of the column in which "a" is. Multiply "a" with this secondary 2x2 matrix obtained and that is the starting time term of the solution.

  2. The 2d term starts with the second element of the summit row (constant "b") accompanied past a negative sign, which at present will multiply a secondary 2x2 matrix which results, once more, from the four elements in the matrix which exercise not belong to either the column of row in which "b" is.
  3. We repeat step 1, but now with the third element from the top row of the matrix.

  And so, the determinant of a 3x3 matrix formula for the full general method is:

  

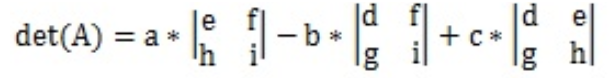
  Equation three: Equation for determinant of a 3x3 matrix through full general method

  The procedure is called an expansion of the first row because every bit you can see in equation 3, all of the elements from the start row of the original 3x3 matrix remain as main factors in the expansion to exist solved for. All of the 2x2 matrices in the expansion are what nosotros call "secondary matrices", and they can be hands resolved using the equation learnt on the determinant of a 2x2 matrix lesson.

  And and then, taking into consideration the formula for the determinant of a foursquare matrix with dimensions 2x2, we can see that equation 3 yields:

  

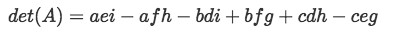
  Equation 4: Equation for determinant of a 3x3 matrix through general method (part 2)

  At this point you may accept noticed that finding the determinant of a matrix larger than 2x2 becomes a long ordeal, but the logic behind the process remains the same and so the difficulty is similar, the only key point is to keep track of the operations you lot are working through, even more than with even larger matrices than a 3x3.

• Shortcut method

  The determinant of a 3x3 matrix shortcut method is a clever trick which facilitates the computation of a determinant of a large matrix by directly multiplying and adding (or subtracting) all of the elements in their necessary mode, without having to pass through the matrix expansion of the offset row and without having to evaluate secondary matrices' determinants.

  The whole process of how to evaluate the determinant of a 3x3 matrix using the shortcut method can be seen in the equation below:

  

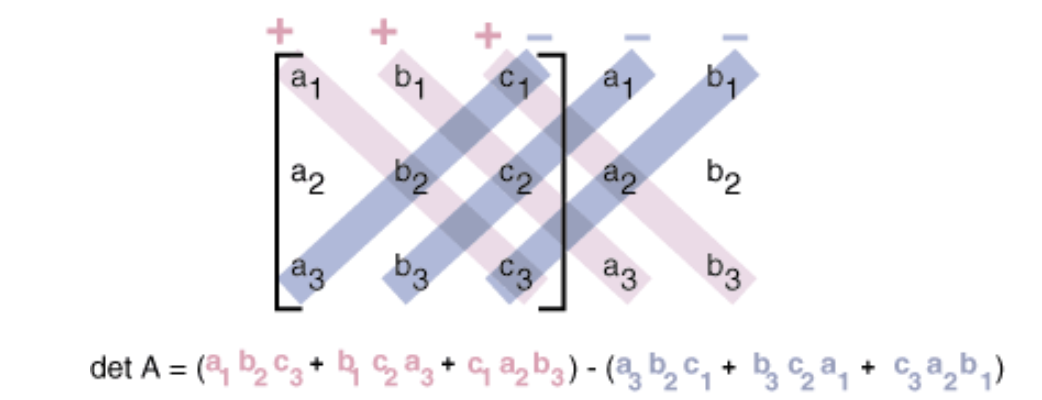
  Equation 5: Shortcut method to obtain the determinant of a 3x3 matrix

  At present let us explain the shortcut method clearly:

  When computing the determinant of an nxn matrix (in this case a 3x3 matrix) as shown above, notice we outset rewrite the matrix accompanied by a repetition of its two offset columns now written outside to the correct hand side.

  Then, the determinant value will be the event of the subtraction between add-on of products from all of the down-rightward multiplications and the downward-leftward multiplications. Said clearer, there will exist a total of iii complete diagonals going from the top left to the lesser correct, and another ready of iii complete diagonals going from the elevation correct to the lesser left.

  We will multiply the elements of each diagonal together, then add together them with the results coming from the other diagonals. There is something to have in listen, all of the diagonals' multiplications going from top left to bottom right have an intrinsic positive sign multiplied to them, while all of the diagonals' multiplications going from tiptop correct to lesser left accept an intrinsic negative sign multiplied to them, and so, when calculation the results from all of the multiplications, a subtraction such as the one shown in equation 5 will result.

  Although this method is simpler to perform than the full general method, it is a niggling complicated to explicate due to all of the multiplications and additions existence worked at the same time, so we recommend you to utilise equation five as a guidance and pay shut attention to the videos where examples of this method are beingness shown.

  In the last section of this lesson we will work through a set of three dissimilar 3x3 matrices and their determinants, nosotros recommend you to compared the processes for both methods to understand them better.

Determinant of a large matrix

The process to evaluate the determinant of a matrix of greater dimensions than 3x3 follows the same logic than what nosotros accept seen so far. Using the general method on a 4x4 matrix A, where its beginning (tiptop) row is conformed by the elements a, b, c and d, we evaluate the determinant of the matrix as follows:

Equation 6: Determinant of a 4x4 matrix

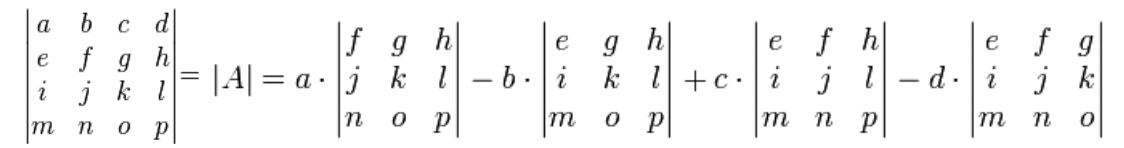
Nosotros in one case more have expanded the determinant by its start row and obtained secondary matrices, which in this case happen to be 3x3 matrices which each can exist expanded and cleaved down into 2x2 matrices. The design in the process repeats, you tin can continue working this manner through even larger square matrices and it will always work, but if y'all are more into the shortcut method, then yous are in for a treat since the method works exactly in the same style as information technology does with 3x3 matrices, it only increases the corporeality of elements yous are working with merely the logic and rearrangement is exactly the same (multiplication from top left to bottom right have a positive sign, multiplications from peak right corner to bottom left have an intrinsic negative sign).

Are yous excited to see how the shortcut method works on larger matrices? We encourage you to try it out on your ain so you can see the whole process. You lot tin ever go dorsum and solve the same matrix using the general method and prove your result is correct.

Exercises on evaluating the determinant of a 3x3 matrix

In the next exercises nosotros will solve the determinant of a 3x3 matrix provided in each instance with the respective method, and at the end we will compare the results obtained.

• Finding the determinant using the General Method
  1. Having the matrix A as divers beneath:

     

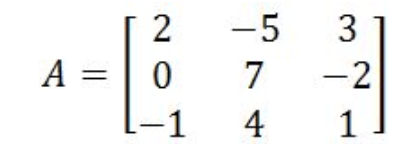
     Equation vii: Matrix A

     Find the matrix determinant using the general method

     For practical purposes we go direct to equation 4 which is a simplification of the formula for the general method shown in equation 3, and and then nosotros apply equation iv to solve all of our exercises corresponding to the general method. Then, the determinant of matrix A is:

     

     Equation 8: Finding the determinant of matrix A

  2. Having the matrix B every bit defined beneath:

     

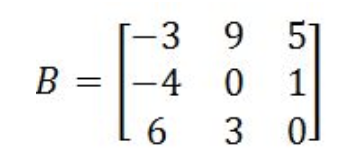
     Equation nine: Matrix B

     Finds its determinant using the full general method:

     

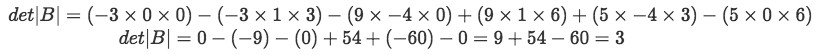
     Equation 10: Finding the determinant of matrix B

  3. Having the matrix C as defined below:

     

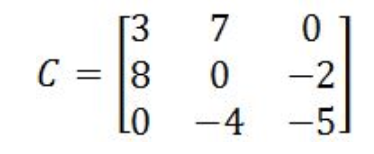
     Equation 11: Matrix C

     Finds its determinant using the general method:

     

     Equation 12: Finding the determinant of matrix C

• Finding the determinant using the Shortcut Method
  1. Having the matrix A every bit defined below:

     

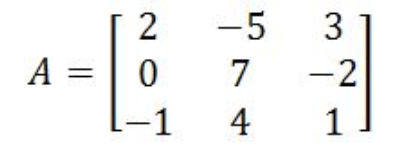
     Equation 13: Matrix A

     Find the determinant of matrix A using the shortcut method:

     Following equation 5, the determinant goes as follows.

     

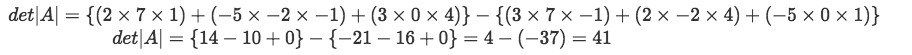
     Equation 14: Finding the determinant of matrix A

  2. Having the matrix B every bit defined below:

     

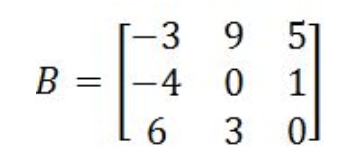
     Equation fifteen: Matrix B

     Finds its determinant using the shortcut method:

     

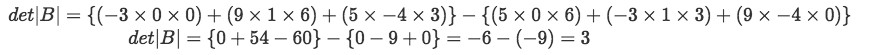
     Equation sixteen: Finding the determinant of matrix B

  3. Having the matrix C as defined below:

     

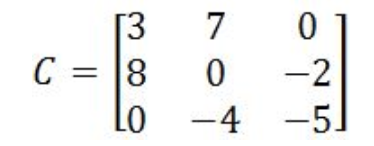
     Equation 17: Matrix C

     Finds its determinant using the shortcut method:

     

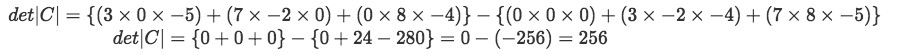
     Equation 18: Finding the determinant of matrix C

Notice that the matrices A, B and C provided in the both sections of exercises higher up are the exact same. This has been done on purpose so you can compare the results from both methods and observe how they yield the same values.

To finalize this lesson we would like to recommend you this article on how to compute determinants and this other one on the determinant of a square matrix, where you will find many more examples than the ones provided here.

We hope this lesson was fun and useful, see you in the adjacent i!

bradleyyournings.blogspot.com

Source: https://www.studypug.com/algebra-help/the-determinant-of-a-3-x-3-matrix-general-and-shortcut-method

Share this post